問題
問99
次のベン図の網掛けした部分の検索条件はどれか。
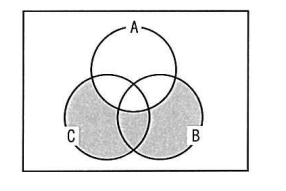
- (not A) and (B and C)
- (not A) and (B or C)
- (not A) or (B and C)
- (not A) or (B or C)
[出典:ITパスポート試験 平成29年度秋期 問98]
正解
正解は「イ」です。
解説
正解は「(not A) and (B or C)」です。ベン図の網掛け部分を見ると、集合Aの内側は一切含まれておらず、Aに含まれない領域だけが対象になっています。さらに、その中でも集合Bまたは集合Cに含まれる部分がすべて網掛けされています。つまり条件としては「Aではない」ことが前提条件となり、その上で「BまたはCに含まれる」ものが該当します。この2つの条件を同時に満たす必要があるため、論理演算子はANDで結びます。
日常の例で考えると、「会員ではない人のうち、東京支店か大阪支店に所属している人」を探すようなイメージです。Aを除外しつつ、BかCのどちらかに該当するものを選ぶ条件になるため、この選択肢が最も適切です。
ア((not A) and (B and C)):
BとCの両方に含まれる部分のみを表しますが、図ではBだけ、Cだけの領域も網掛けされているため条件が狭すぎます。
ウ((not A) or (B and C)):
Aでない全ての領域が含まれてしまい、図で網掛けされていない部分まで条件に含まれるため不適切です。
エ((not A) or (B or C)):
A以外の領域がほぼ全て対象となり、網掛け範囲よりも広くなってしまうため図と一致しません。
難易度
本問題は、ベン図と論理演算子の関係を正しく読み取れるかが問われる基礎レベルの問題です。図の意味を文章に置き換える力が必要なため、初心者にはやや戸惑いやすいですが、ANDとOR、否定の意味を一つずつ整理すれば比較的解きやすい内容です。
用語補足
ベン図:
集合の関係を円で表した図です。条件の重なりを視覚的に確認できます。
AND:
複数の条件をすべて満たす場合に成立する論理演算です。「かつ」に相当します。
OR:
いずれか一方でも条件を満たせば成立する論理演算です。「または」を意味します。
NOT:
条件を否定する演算です。「~ではない」という意味になります。
対策
ベン図の問題では、いきなり式を考えずに「どの円の内側・外側が塗られているか」を言葉で説明する練習が有効です。その後、「~ではない」「かつ」「または」に対応するNOT、AND、ORに置き換えることでミスを防げます。特にANDとORの違いは頻出のため、日常例と結び付けて理解しておくことが重要です。



