問題
問33
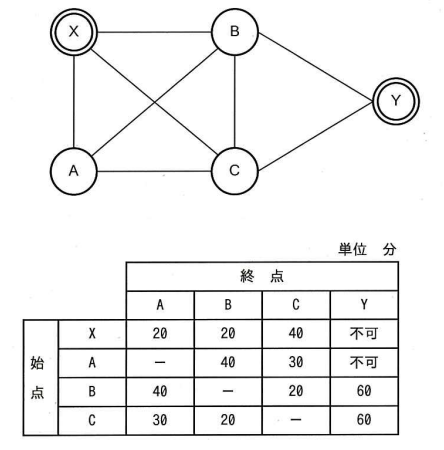
地点Xから出発してA, B, Cの3地点の全てを経由して地点Yまで行きたい。各地点間の経路と所要時間が図及び表のとおりであるとき、地点Xから地点Yまで行く最短の時間は何分か。ここで、3地点A, B, Cはどのような順番で経由してもよいものとする。
- 110
- 130
- 140
- 150
[出典:ITパスポート試験 平成28年度春期 問33]
正解
正解は「イ」です。
解説
正解は130分です。 この問題は、与えられた地点間の所要時間を使って、X地点からY地点までA、B、Cの全ての地点を経由する最短経路を求める問題です。まずは、A、B、Cのどの地点から始めて、どの順番で経由してY地点にたどり着くかを全てのパターンで確認し、それぞれの合計所要時間を計算します。 表を確認すると、XからYへ直接、AからYへ直接は行けないことが「不可」と示されています。BからYへは60分、CからYへは60分で行くことができます。 考えられる有効な経路は以下の通りです。
- X → A → B → C → Y: 20 (X→A) + 40 (A→B) + 20 (B→C) + 60 (C→Y) = 140分
- X → A → C → B → Y: 20 (X→A) + 30 (A→C) + 20 (C→B) + 60 (B→Y) = 130分
- X → B → A → C → Y: 20 (X→B) + 40 (B→A) + 30 (A→C) + 60 (C→Y) = 150分
- X → C → A → B → Y: 40 (X→C) + 30 (C→A) + 40 (A→B) + 60 (B→Y) = 170分
その他の経路は、AからYへ直接行けないため、途中でAを経由しYへ向かうルートは成立しません。
例えば「X → B → C → A → Y」のような経路は、A→Yが不可なので選択肢から除外されます。 これらの計算結果を比較すると、最も短い所要時間は2番目の「X → A → C → B → Y」経路の130分となります。このように、全ての有効な経路を洗い出して、それぞれの合計所要時間を計算し、一番短いものを選ぶのがポイントです。
ア(110):
110分は、上記の計算結果には見られず、A,B,C全ての地点を経由するという条件を満たす最短時間ではありません。
ウ(140):
140分は、「X → A → B → C → Y」という経路の所要時間ですが、これよりも短い経路が存在するため、最短ではありません。
エ(150):
150分は、「X → B → A → C → Y」という経路の所要時間ですが、これよりも短い経路が存在するため、最短ではありません。
難易度
この問題は、与えられた条件に基づいて複数の経路を計算し、最短のものを見つけ出す「最短経路問題」です。複雑な計算式は不要ですが、全ての可能性を漏れなく検討する根気と正確さが必要です。特に、表の「不可」という条件を見落とさずに計算に含めることが重要で、初学者にとっては少し戸惑うかもしれません。一つ一つ丁寧に計算すれば解ける、中程度の難易度の問題と言えるでしょう。
用語補足
最短経路問題:
ある地点から別の地点へ移動する際に、最も時間やコストがかからない経路を見つける問題です。例えば、地図アプリで目的地までの最短ルートを検索するのも最短経路問題の一つです。
ノード:
ネットワーク図やグラフ理論において、地点や場所を表す点のことを指します。この問題では、地点X、A、B、C、Yがそれぞれノードにあたります。
エッジ:
ネットワーク図やグラフ理論において、ノード(点)とノードを結ぶ線のことを指します。この線は、通信経路や道、関係性などを表し、この問題では地点間の経路がエッジにあたります。エッジには、時間やコストなどの重みが設定されていることが多いです。
グラフ理論:
点(ノード)と線(エッジ)で構成される図形(グラフ)の性質を研究する数学の一分野です。交通網のルート最適化や、SNSでの人間関係分析など、様々な分野で応用されています。
対策
この問題のポイントは、A, B, Cの3地点を全て経由するという条件と、表の「不可」の情報を正しく解釈することです。まずは、XからYへA, B, Cを巡る全ての有効な順番(順列)を書き出します。次に、それぞれの順番について、表に示された所要時間を足し合わせて合計時間を算出します。この際、表の「不可」と記載された経路は利用できないため、計算から除外するか、その経路を含むルートを無効と判断します。全ての合計時間の中から最も小さい値が最短時間となります。一つ一つ丁寧に計算することで、ミスなく正解にたどり着くことができます。




